こんにちは!ぺそです。
さて、みなさんは受験やテスト勉強を通して、三角形の面積の求め方から、二次方程式の解の公式といった複雑なものまで、沢山の公式を覚えてきたと思います。
こういった公式は覚えていると問題を解く上で、とても役に立ちますが、一方、単なる受験のテクニックとして教わっていたり、そのまま公式を覚えるだけの人が多いな感じます。
試験だけを主眼をおいた場合、これでも良いのかも知れません。けれど、それだと社会人になったときに、その労力は無駄に終わります。
そこで、今回はなぜ丸暗記が危険なのか、丸暗記をするとどういうデメリットが有るのか、逆に丸暗記したほうがいいときはどういうときなのかについて書きたいと思います。

せっかく頑張って身につけた公式が「受験でしか使い物にならなかった!」なんてならないように、ぜひ参考にしてみてね
例:三角関数の公式
まずは、実際に公式を丸覚えしないケースを見てみましょう。ここでは三角関数を例にして見てみます。
「三角関数」とは
※ 三角関数についてよく知っている方は、こちらまでスキップしてください。
三角関数について知らない人のために補足すると、三角関数とは「一つの角の大きさが他の線分の長さとの関係を表す関数」のことです。・・・よくわからないですよね?(笑)
例で見るとわかりやすいので、下の解説と図を見てください。
xy 軸の平面に原点を中心として、半径1の円を書きます。このとき中心からある角度(ここではθと置きます)の線を、原点から円の外周に当たるまで引きましょう。
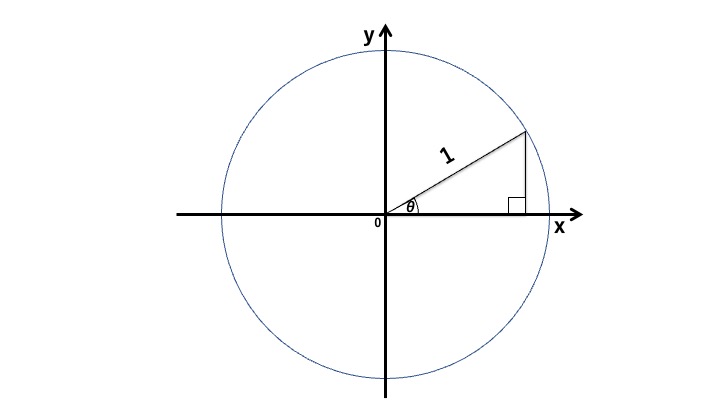
伸ばした直線と円の外周の交点から x軸に垂線を下ろしましょう。そうすると、三角形が出来ますね。
この三角形に着目すると、角度が決められていれば、斜辺に応じて、他の辺の長さが決まることがわかります。
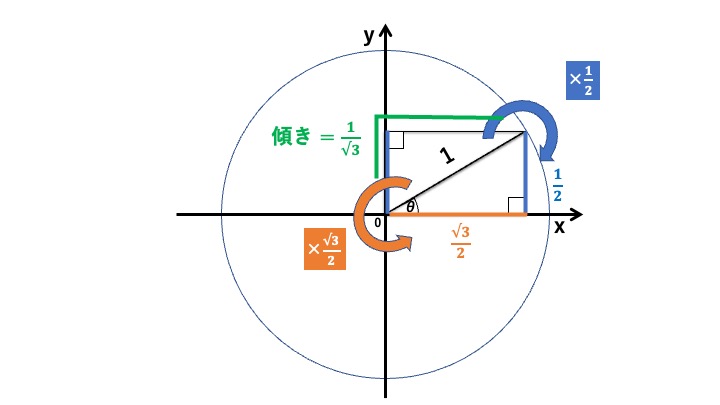
今回のθという角度では、斜辺の1/2が高さ(y軸の値)に、斜辺の√3/2が底辺(x軸の値)になりました。
このように角度が一つに決まれば、斜辺から x座標、y座標、直線の傾きを計算することができるのです。これが三角関数です。
三角関数では「×1/2」のところをサイン(sin:正弦)、「×√3/2」のところをコサイン(cos:余弦)、この斜辺の傾きである「1/√3」をタンジェント(tan:正接)と呼びます。式で書くと、こんな感じですね。
sinθ = 1/2
cosθ = √3/2
tanθ =1/√3
※ ちなみにこのときのθは 30°が一つの正解になります。

ちなみに、三角関数はギリシャから生まれ、当時はサインの概念として jiva と呼ばれていました。後々それがヨーロッパに伝わっていく中で、sinus(ラテン語で「凹所、入江」の意味)→ sine → sin になりました。
実はこのとき、cos は存在しておらず、sin の概念を知ったインド人が「ならば余りの角にもサインがあってもいいのでは」と考え、余った角のサインを cotijiva と名付け、sinus complenti → co-sine → cos というふうになりました。
日本語でコサインを「余った弦」と表すのは、そういった意味からなんですね。
三角関数の余角/補角の公式
三角関数には、この定義をスタートにして、沢山の公式があります。ここではその中の余角・補角の公式を見てみましょう。
余角の公式:
sin(90°−θ) = cosθ
cos(90°−θ) = sinθ
tan(90°−θ) = 1/tanθ
補角の公式:
sin(180°−θ) = sinθ
cos(180°−θ) = −cosθ
tan(180°−θ) = −tanθ
これ、全部覚えるのはすごい大変そうですよね・・・。けれど、定義からしっかり自分で理解していれば、実は覚える必要無いんです。
単位円を見れば、一目瞭然
先ほどと同様に単位円を書いて考えてみましょう。ここでは「cos(180°-θ) = -cosθ」がなぜ成り立つのかについて見てみます。
まず、求めたいのは cos(180°-θ)ですから、その角度で直線を引かないといけません。ちょうど x軸の直線が 180°なので、そこからθ分引いた直線を引きましょう。
実際にそれを引いてみたのが、下記の図です。
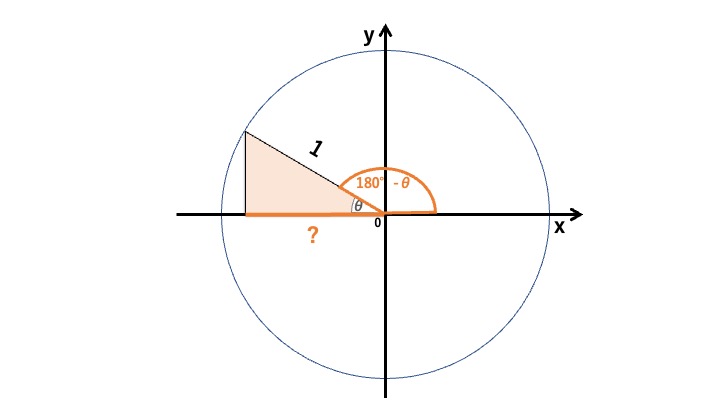
求めたいのは、このオレンジの「?」ところです。ここでθを角にする直角三角形を右側に追加してみましょう。ちょうど y軸を対称軸にする感じです。
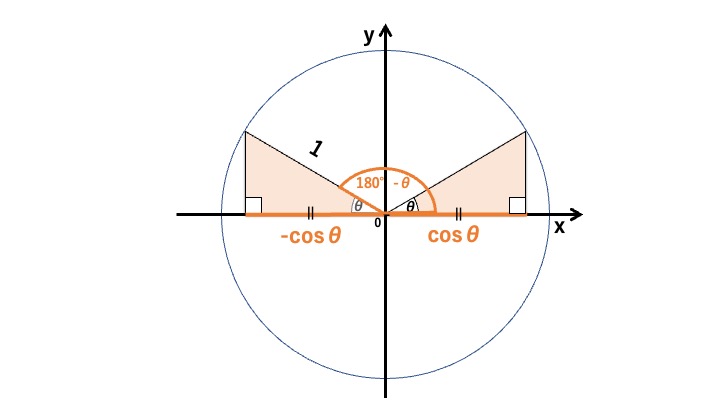
こうすると、オレンジの三角形2つは合同であることがわかります。したがって x軸と重なっているオレンジの線も2つとも等しくなるので、x軸の長さはどちらも cosθになります。
x軸を挟んで反対側に伸びているということは、マイナスの値を取るので、cosθではなく、-cosθが値となります。
したがって、「cos(180°-θ)= -cosθ」が成り立つのです。
他のケースも同様に説明できるので、実際に線を書いてやってみてください。公式が成り立つのが分かると思います。
このように単位円を書いておけば、上記の余角・補角の公式は覚える必要がありません。しかも、定義から自分で導いているので記憶ミスをすることも無いでしょう。

自分も三角関数が関わる試験のときには、真っ先に単位円(半径が1の円)をテスト用紙の隅っこに書いてから解き始めていたよ
「丸暗記をしない」ことで鍛えられていく能力
それでは、いよいよ本題です。三角関数の例を通して、公式は丸覚えするのではなく、自分で導けることがわかりました。
では、公式を自分で導くことが出来ず、丸覚えする癖がついてしまうと、どんな能力を身に着けられなくなってしまうのでしょうか?
① 物事の本質を意識する
まず、丸暗記ばかりしていると、物事の本質がわからなくなります。丸暗記している項目は、ただの文字情報の羅列に過ぎず、意味を持たないからです。
一方丸暗記せずに、きちんと意味や背景を理解し、自身の言葉で証明・説明できる人は、その事の本質を知っています。
たとえば、皆さんが新しいお菓子を開発・発売する立場になったとしましょう。そのときには市場に受け入れられるために、競合を分析しないといけませんが、このときどういった企業や商品を競合として調査しますか?
名だたる菓子メーカーは沢山います。グリコ、ブルボン、ロッテ、森永製菓、不二家・・・そういったところと差別化することを考えるかもしれません。
しかし、皆さんがどういった菓子を作るかで競合は全く異なるはずです。
例えば、お酒のおつまみになるようなお菓子を考えるなら、競合は同じおつまみ製品を出している菓子メーカーではなく、塩辛メーカーや、スーパーの惣菜、果ては居酒屋でしょう。
高級感のあるお菓子なら、競合は高級フレンチのデザートや近くのケーキショップ、はたまた喫茶店かも知れません。

このようにお菓子という表面上のジャンルをなぞっているだけでは、顧客に価値は届きません。どういった価値をお菓子を通して顧客に与えるのかという深い洞察が必要です。
公式を丸覚えしてしまうと、この深い洞察をする機会を失ってしまいます。結果、このケースはこう、このときはこう、という限られたケースでの対応しかできなくなっていくのです。
社会人になっても、3Cや4P、5フォース分析、ビジネスモデル・キャンバスなど、様々なフレームワークを利用します。
けれど、それらはあくまで過去の英知から導き出された公式であって、なぜそれをこのときに使うのかを意識しないと上手く使えません。
それらは手段であって、目的では無いからです。

今まで多くの人の施策のレビューをしてきたけれど、これが出来る人は本当に少ないと思う。
「言われたから」「周りが使っているから」という人のほうが圧倒的に大多数で、だからこそ折角の施策もあんまり効果が出ないで終わるケースを沢山見てきたよ。
② 応用力が鍛えられる
さきほどの単位円の例では、90°-θや 180°-θのケースを見ましたが、では270°-θではどうでしょうか?あるいは、θ+90° だったら?
公式を丸暗記していると、「そんなの覚えていない!」となって撃沈してしまいます。しかし、単位円から導き出す方法がわかっていれば、なんの問題もありません。
このように核となる事柄から応用的に考える能力が、丸暗記ばかりしていると失われていきます。
社会人になっても同様です。就いた職種、例えばルーチンワーク系の仕事で良ければ、応用力はそこまで求められないかも知れません。けれど、そういった職種は誰であっても可能な仕事が多く、簡単に代替可能なので、給与はお世辞にもいいとは言えません。

また、時代は変わっていくものです。昔の常識は今の常識ではありませんし、今の常識が将来の常識にはなりません。
しかし、その常識が生まれた背景をきっちり理解していると、この先の変化にも対応出来るはずです。
今後「人生は100年時代」と言われています。自分の父の世代では定年は 60歳でしたが、今後は 80歳まで働かないといけなくなるかもしれません。そもそも定年制さえ廃止される方向に進んでいます。
そんなときに「定年まで働いて退職金を得てリタイアする」という公式が通用するでしょうか?
この公式が、戦後日本から今に至るまで成立していた理由を知っていれば、すでに対応に向けて動く事ができます。なぜなら、この公式の前提が既に崩れている事を知っているので、この公式は今後成り立たないことが分かるからです。
③ 脳のキャパシティが節約される
物事には覚えていないと、どうしようもないものもあります。
英語ではそれが単語だったり、国語だったら漢字だったり、理科だったら元素記号だったり。
学校の勉強に限っても、覚えることが沢山ありますから、覚えていなくてもいいことは極力覚えない方が脳を有効に使えます。
単純に考えると、単位円からの導き方がわかれば、余角・補角の公式 6つは覚えなくても問題ありません。その空いた 6つを英語の単語に費やしたり、数学の別の覚えておかないと難しい公式に費やせばいいわけです。
二次方程式の解の公式でさえ、自分は最初は覚えていませんでした。なぜなら、平方完成さえ知っていれば、覚えていなくたって問題を解くことは出来るからです。
そして、平方完成のほうがよっぽど応用力があります。
平方完成ができれば、、、
・二次方程式の解を求められる
・二次関数のグラフの頂点の座標を求められる
・各種証明や計算問題が解ける(正の数である証明など)
ただ、ここで誤解してほしくないのですが、「覚える量を極限まで減らそう!」というのも正しくありません。
ここで伝えたいのは、応用力が効くような本質的なところを覚えておき、枝葉の細かい部分は覚えないということです。
公式丸暗記が有効な場合
とはいえ、丸暗記が絶対に駄目かというと、そんなことはありません。例えば、次のような場合は丸暗記しておいたほうがいいでしょう。
① 公式を導き出す過程が長すぎる
1つ目は「その場で公式を導き出すのに多大な時間がかかる場合」です。先程の三角関数の例では、90°-θのケースは単位円を書いてサクッと導き出せます。
しかし、次の公式を短い時間で導くのは、かなり厳しいでしょう。
ド・モアブルの定理
n が整数のとき、
(cos𝜃+𝑖sin𝜃)𝑛=cos𝑛𝜃+𝑖sin𝑛𝜃
こういったケースでは公式を覚えていたほうが、圧倒的な時間短縮に繋がります。
日常生活で例えると、災害時の対応が分かりやすいかも知れません。
例えば、家にいるときに大きな地震が発生したら、窓や戸を開けて出口を確保する必要があります(ただし身の安全が第一で、揺れが収まってからでも良い)。
これは、地震の最中に窓や扉が変形して、家から出られなくなるケースがあるからです。たとえ最初の地震で対応できなかったとしても、地震は連続的に起こることがあるため、次の余震に備えておくわけです。
もし、地震が起きたときに「えっと、地震が起きたってことは、大きな力が家に加わるんだ。そうすると、扉が変形して家から出れなくなるかも。扉を開けないと!」と導き出してるようでは、命が危険にさらされてしまいます。

② 何度も使っているうちに自然と公式を覚えた
もう1つは単純に「何度も使っているうちに覚えてしまった場合」です。
例えば、三角形の面積は「他底辺×高さ×1/2」であるとか、直角二等辺三角形の辺の比は 「1:1:√2」だとかは、何度も何度も出てくるうちに自然に覚えてしまっている事が多いと思います。
無理に忘れるのは本末転倒ですから、こういう場合も公式を覚えていても問題ないでしょう。
ただ、どちらも公式を自らの手で導き出せることが大事なのは変わりません。

先に話に出ていた二次方程式の解の公式も、自分は実際覚えちゃってたなー。公式を暗記していること事態は、なんにも悪くないよ!
まとめ:公式丸暗記から卒業して、将来につながる力を手に入れよう
いかがでしたでしょうか?丸暗記はたしかに便利ですし、非常に有用に働くケースもあります。
けれども、物事は何事もトレードオフです。丸暗記することと引き換えに失っているものがあることに気づいてもらえたら、嬉しいです。

もし、みんなが過去学んだ公式の中で「あれ?これ自分の言葉で成り立つ理由が説明できないぞ」となったものがあったら、是非もう一度証明をおさらいしてみてください!