こんにちは、ぺそです!今日のテーマは「角度」についてです。
皆さんはいままで色々と角度を求めて来たんじゃないかなと思います。当たり前のように 30° 0-60°-90°直角三角形定規を使ったりもしますよね。
けれど、なぜ「360°なの?」という質問に答えられる人は、なかなか少ないと思います。そこで、今回はこの質問に2つのアプローチ方法で答えていきましょう!
まずは「角度」の定義を確認
まずは、角度を測る「度」という単位に関してみてみましょう。こちらは、日本の経産省が出している計量法体系において、次のように定義されています。
度 = 「円周を三百六十等分した弧の中心に対する角度」
経済産業省 計量法体系(p.12 より)
つまり、円を360分割したときの1つを1度と定義しているんですね。
これは「定義」なので、なぜそれが度となるのかは証明できません。(定義に関しては別記事で詳しく書いているので、そちらをごらんください
しかし、定義であっても「なぜ?」は重要です。なぜなら、定義は「そうした方が人間にとって都合がいいから」そうしているのであって、適当に決まったわけではないはずです。
では、なぜ円を 360 分割に区切るようにして角度を決定したのでしょうか?
① 逆に考える ~ もし100度だったら ~
こういうときは、逆に考えてみましょう。つまり「もし円が360度じゃなかったらどうなるのか」を考えるわけです。
真っ先に思いつくのは 100度だと思います。分かりやすいし、覚えやすいし、キリもいいですよね。では、これで代表的な 2つの三角形の角度を表してみましょう。
三角形のの内角の和は本来 180 度(円の角度の半分)になるはずですが、今回は円の角度を 100度にしているので、50度になるはずです。
では実際に計算してみますね。すると下記のようになります。
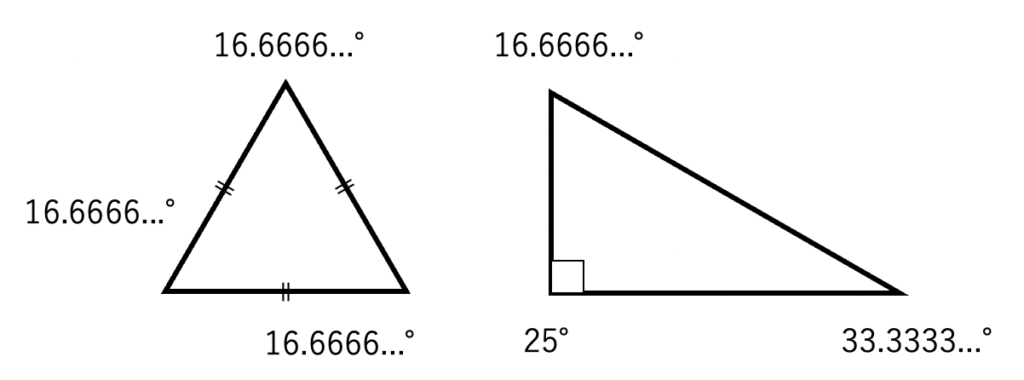
一気に分かりづらくなってしまいましたね・・・360度のときはこんなこと起こらなかったのですが、なぜなんでしょうか。それは「360」という数字に秘密があります。
360 という数字は「約数」が多い
360 という数字は、実は便利な特徴があります。それは「いろいろな数で割り切れる」つまり「約数が非常に多い」ということです。試しに先程例に出した 100 と比べてみましょう。
100の約数:1, 2, 4, 5, 10, 20, 25, 50, 100 → 9個 360の約数:1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360 → 24個
100の約数の 2倍以上あります。これは、単純に数が 100より多いからではありません。例えば、400 の約数も書いてみます。
100の約数:1, 2, 4, 5, 10, 20, 25, 50, 100 → 9個 360の約数:1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360 → 24個 400の約数:1, 2, 4, 5, 8, 10, 16, 20, 25, 40, 50, 80, 100, 100, 200, 400 → 15個
結果、360の方が約数が多いですね。約数が多いということはそれだけ割り算がしやすいのです。つまり色々な計算で便利に使うことができるんですね。
360 という数字は「7」以外の一桁なら割り切れる
もう一つ非常に便利なポイントは、「一桁であれば 7 以外全てで割り切れる」という点です。いくら約数が多くてもそれが例えば 13 とか 27 とか、普段使いにくいような数だと困ります。
その点、360 は非常に優秀で、7以外であれば簡単に割り切れるわけです。
ちなみに 「1~9 全てで割り切れる数だともっと便利では?」と考えたので、ちょっと探してみると、「2520」がその数になりました。
ただ、これだとサクッと計算とは行かないですし、数も大きくなり過ぎています。もし 2520 が円の角度だった世界線があったしたら、分度器の目盛りなんか、ものすごく細かくて、肉眼では確認できないでしょうね(笑)
② 起源を考える ~ 360という数字はどこからきたか ~
先程までは、どちらかというと「便利」という点を見てきましたが、起源を考えるのも良いポイントです。例えば、漢字にも象形文字という起源があったりしますよね。
というわけで、360 の起源を探るためには、時計がない時代にまで戻ってみましょう。
時計がない時代に、どうやって人々は時間を図っていたのかというと、太陽の高度を使っていました。有名な日時計ですね。太陽が作る陰の場所で、おおよその時間を測ることができます。
太陽暦で太陽が戻るのは 365日
太陽が一周する期間を 1日と定義した場合、日によって太陽の高さが上下していることに当時の天文学者は気づきました(日本だと夏は太陽が高く、冬は低いですよね)。
そこで太陽が再び同じ場所に現れる日を数えると、365日だったんです(太陽暦)。

ちなみに、太陽暦は現在みんなが使っているグレゴリオ暦のベースになったものだよ!
太陰暦で月がもとに戻るのは 355日
さて、昼間は太陽があるからいいですが、夜はどうすればいいのかといえば、月がありますね。同様に月が同じ位置に戻ってくるのにかかる期間を数えると、こちらは、355日でした(太陰暦)
太陰暦は残念ながら現在は使われていません。なぜかというと、季節の循環は太陽との関係でできるので、月に関しては無関係だからです。従ってこちらを使ってしまうと、数年前は 5月が暑くて、数年後は 11月が暑いみたいになってしまうからです。

季節は太陽に取られたけど、海の潮の満ち引きは月の引力に寄って起きるんだ。だから、もし人類が温度よりも潮の満ち引きに影響を受ける存在であれば、太陰暦が使われていたかもしれないね
太陽暦 + 太陰暦 / 2 = 360
さて、この1年の月や太陽の動きがどうやって引き起こされているか、皆さんは御存知ですよね。そうです、それぞれの惑星の自転や公転によって起こされています。つまり円を描く運動なんです。
この円を1週する運動にかかるのが365日と355日だったので、間をとって360日とし、これを角度としたんですね。
【まとめ】360は数値として利用しやすく、太陽暦を起源にしていた
これで起源の面でも、利用用途の面でも、なぜ円が360度なのか理解できたと思います。
このように「あたりまえ」として受け入れているものに対して、「なぜ」と考えるのは非常に良いことです。実際社会においても「あたりまえ」を疑うことから、革新的なビジネスが生まれています。
- なぜ「リンスとシャンプーは別々なのか?」=> リンスインシャンプー
- なぜ「お店で商品を買わないといけないの?」=> 通販サイト
- なぜ「本は紙じゃないといけないの?」=> 電子書籍
ちなみに定義の理由について考えるのは、別に好きなものからでもいいと思います。
なぜ「バスケは2点が基本なのか」、なぜ「将棋の歩兵は成ると「と」になるのか」・・・是非「なぜ」に蓋をせずに、自由に考えたり、調べたりして見てくださいね!

もし興味が湧いたら、次の本を読んでみると面白いかも。ただ面白い雑学じゃなくて、ビジネス方面に役立つようなコンテンツが入っているから、知っておくだけでも、役にたつと思うよ!