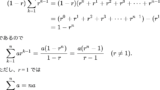皆さんは、下記の状況になったとき、どういう判断を下しますか?
"最近 Youtube で動画投稿を始めたあなたは、かなり順調に登録者数を稼ぎ、半年たった今では 5000人になりました。視聴者数も伸び、さらに視聴者に良い動画を届けたいと思っています。そんなとき、ある有名な芸能人とコラボする案が出てきました。とはいえ、向こうは芸能人で、ゲストとしてお呼びするには 10万円かかります。"
この場合、あなたはゲストを呼んだほうがいいと思いますか?
こんにちは、ぺそです!この前、学生時代の数学の知識が役に立ったので、ここで紹介したいと思います。役に立った公式は等比数列です。何に役に立ったのかというと、「このサービスをユーザーはどれくらい使い続けてくれるのか」の算出のためです。
今回の知識を身に付けると、皆さんが将来社会人になってお金を稼ぐことを考えるときに、とても参考になるはずです。是非最後までお付き合いください。(今回は少し長くなりそうなので、前後編になります)
等比数列のおさらい
まずは、復習を兼ねて等比数列を確認しましょう。等比数列の定義は非常にシンプルです。「ある特定の数字に一定の数をかけ続けてできた数列」。それだけです。例えば、
① 3, 6, 12, 24, 48…
② 1, 4, 16, 64, 256…
①は「3」に何度も「2」を掛け算してできた数列ですし、②は「1」に何度も「4」を掛け算してできた数列になります。この最初に掛けられる数を「初項」、何度も掛ける数を「公比」といいましたね。
このように規則性がある数列の場合、何番目に何がでるか予測できそうですよね?例えば ②の数列を掛け算の形に直すと、
1番目:1 × 0
2番目:1 × 4
3番目:1 × 4 × 4
4番目:1 × 4 × 4 × 4
5番目:1 × 4 × 4 × 4 × 4
となります。じゃぁ、もし n 番目だったらどうでしょう?上のままだと気づきにくいので、整理し直すと、
1番目:1 × 0
2番目:1 × 41
3番目:1 × 42
4番目:1 × 43
5番目:1 × 44
と表せますね。特定の数の 0乗は 1 にするという定義があるため、一番上も 40と考えると、「あれ?何番目の数と掛ける回数が【一つずつ】ずれているだけ?」ということに気がつくと思います。であるならば、n番目は、下記のようになることが予測できますね。
n番目:1 × 4n-1
最初の数である初項を a、何度も掛ける数である公比を r と置くと、
n番目:a × rn-1
はい、これが等比数列の n番目(一般項といいます)を求める公式になります。勿論本当に成り立つのかの証明が必要ですが、それは今回は割愛します。
サブスクリプションモデル
続いて、ユーザーの平均サービス利用時間の方に行きましょうか。実はこれ、とても重要なんです。
最近のサービスでは継続して毎月お金を払うタイプのものが多いと思いませんか? Netflix、Spotify、Amazon Prime、Youtube Premium… どれも毎月決まった額を継続して支払うサービスですよね。これを「サブスクリプション(subscription)サービス」と呼びます。略して「サブスク」とも言われることも。英語だと難しいですが、簡単に言うと定額制です。なので、携帯の通話料も立派なサブスクビジネスです。
さて、そんなサブスクは今までのビジネスモデルとは大事なポイントが違います。例えば、Switch のゲームソフトやテニスラケットなどの買い切り型の商品は「買ってもらう」のが勝負です。一方サブスクは「続けてもらう」のが勝負です。一般的にサブスクは定額な分、値段が抑えられているので、毎月継続してもらって初めて利益が出るからです。
平均利用期間 = ユーザーがどれだけ使ってくれるか?
そうなると、大事なのは「このユーザーはどれだけの期間、うちのサービスを使ってくれるんだろう?」ということです。
例えば、Netflix では映画制作費、配信サービスの開発費用、プロモーション広告に、毎月 40億円かかるとします。ユーザー数が 1000万人、ユーザーは500円/月払うものとした場合、毎月の売上は 50億円になり、利益として 10億円が入りますね。
10億円も儲かるなんてすごい!…とはならないのがサブスクです。仮に Netflix ユーザーは平均して半年でサービスを解約してしまうとしましょう。そうすると、1年間の収支を見ると、
費用:40億円 × 12ヶ月 = 480億円
売上:1000万人 × 500円 × 6ヶ月 = 300億円
というわけで年間ではマイナスになってしまいました。こうなると、「費用を抑える」「ユーザー単価を上げる」「ユーザーに長く居てもらう工夫をする」「解約以上の新規ユーザーを獲得する」など、いろいろな手を考えないと行けないでしょう。
※ もちろん、これは極端な例ですし、数値は実際に異なります(実際の Netflix ユーザーは、2021′ 8月時点で 2億900万人います)
サービス初期では、平均利用期間は分からない
今回のケースであれば、平均利用期間が出せましたが、例えばこの記事の最初に書いたようなケース、つまり「始めてからあまり月日が経っていない場合、平均利用期間が分からない」という事態になってしまいます。
これはどういうことかというと、仮にAさんとBさんがいたとして、Aさんは 2年で、B さんは 6年でサービスを辞めた場合、このとき平均利用期間は 4年と出すことができます。
ですが、もし今サービスを開始して 4年目だった場合は、どうでしょう?
この場合、Aさんは 2年で辞めているので問題ないですが、Bさんは4年目で、まだ使っています。この場合、平均利用期間は 3年となってしまい、本来より短く算出されてしまいます。
これでは正確な判断ができません。かといって、まさか全員が辞めるまで待つわけにも行きません。さてさて、どうしたものか・・・とここで役立つのが、「等比数列」と「解約率」の考え方なのです。