「十分に時間を取って、何度も何度も見直したのに、返ってきた結果を見たら 予想より10点以上低かった・・・・」
こんな経験をした人はいませんか?自分も最初のころは良くそういった経験をしていました。
ケアレスミスで受験に失敗したり、悔しい思いをした人もいると思います。
では、なぜこういったミスをしてしまうのでしょうか?
特に受験では、今後の数年間がかかっているわけですから、それこそ目を皿のようにして、ミスは無いかチェックしているはずです。
それでもミスは起きてしまうものです。
今回は見直しの質を上げてケアレスミスを防ぐために、「確証バイアス」という考え方についてご紹介します。

自分も、この記事で紹介する方法を身につけることで、点数が格段にあがったよ。この記事で少しでもみんなの見直し間違いが減って、点数が上がると嬉しいな
実験:「2,4,6」挙げられた数字の規則を見抜け
まずは、今回紹介する「確証バイアス」について説明するために、皆さんにも実験に参加してもらいましょう。下記の数字を見てください。

さて今、3つの数字を皆さんの前に提示しました。
皆さんにやっていただきたいのは、この数字がどのようなルールで並んでいるかを当てていただくことです。
とはいえ、この情報だけでは正解することが難しいので、ルールを確かめる方法が1つ与えられています。
それは、次に続く数を予測し、それが正しいかどうかを聞くことが可能だということです。
もし、その数がルールに当てはまっていれば、「ルールに一致」と答えが返ってきます。もし、その数がルールに当てはまっていなければ、逆に「ルールに不一致」と返ってくるというわけです。
また、この質問は何度していただいても構いません。ただし、どのようなルールか当てるのは一回のみとします。
さて、皆さんはどんな数を聞いてみますか?

実際のテストでも、見直し自体は何度もできるけれど、一度答えたら(提出したら)それ以上は何もできないところが、今回の実験と一緒だね。
「最後の数に2を加えた数字」は間違い
残念ながら、記事上で皆さんの質問に答えることはできないので、ここでは、この実験が行われたときに挙げられた数字とルールを下記にご紹介しましょう。
【挙げられた数字】
「8」→ 一致
(8の後に)「10」→ 一致
(10の後に)「12」→ 一致
(12の後に)「14」→ 一致
【予測されたルール】
「ルールは、最後の数に2を加えた数字」
→ 不正解
「あれ?」と思った方が多いのではないでしょうか?自分も最初はそう思いました。けれど、正解は違うのです。
実際の実験でも、ほとんどの被験者が「最後の数に2を加えた数字」がルールだと思い、間違えたようです。
※ 参考までに、もし自分が被験者だったら試したであろう数字と予測したルールについても、下に書いておきます。
【挙げられた数字】
「12」→ 一致
(12の後に)「14」→ 一致
(14の後に)「16」→ 一致
【予測されたルール】
「ルールは、3つ前の数に10加えた数字」
→ 不正解
【挙げられた数字】
「20」→ 一致
(20の後に)「40」→ 一致
(40の後に)「60」→ 一致
【予測されたルール】
「ルールは、3つ前の数を10倍した数字」
→ 不正解
【挙げられた数字】
「22」→ 一致
(22の後に)「44」→ 一致
(44の後に)「66」→ 一致
(66の後に)「222」→ 一致
【予測されたルール】
「ルールは、3つ前の数の一桁目を、最終桁に追加した数字」
→ 不正解

鋭い人は、上位の不正解のルールから、なんとなく解答を思いついてきたかもね
このルールの正解は・・・
しかし、ここで非常に賢い学生が全く異なる方法で、この課題に取り組みました。彼が聞いた質問はこちらです。
【挙げられた数字】
「4」→ 不一致
「7」→ 一致
「-4」→ 不一致
「9」→ 一致
「-3」→ 不一致
このように、この学生はルールに当てはまらない数字をたくさん確かめていきました。そうして、彼はついに答えを導き出したのです。
【予測されたルール】
「ルールは、次に来る数字は前の数字より大きい数字」
→ 正解
いかがでしょうか?確かに過去にあげた数字はすべてルールを満たしています。そしてルール自体は非常にシンプルなものでした。
正解した学生だけは「自分の間違い」を証明しようとしていた
では、この正解できた学生と間違えた学生たちの違いは、何だったのでしょうか?
違いは明確です。不正解の学生は、自分が予測したルールに当てはまる数字を上げて、自分のルールの正しさを確かめようとしていました。
挙げられていた数字はすべてルールに一致していましたが、逆に言うと「間違っているかも」という情報が一切入っていませんでした。
一方正解した学生は、自分が予測したルールに当てはまらない数字を上げて、自分のルールの間違いを確かめようとしていたのです。
こちらの学生は「不一致」という答えをもらうことで、自身のルールの思い込みに嵌まらずに済んだのです。そして、この間違いである証拠を意図的に探していたのがポイントです。
つまり、ほかの学生たちは「自分の推測の正しさを証明するもの」を見つけようとしていたのに対し、賢い学生は「自分の推測の誤りを証明するもの」を探していたわけです。
これが確証バイアスの恐ろしさです。
確証バイアスは至るところにある
人は無意識に自分にとって都合がいい(正しい)と思えるような情報を集める傾向があります。これを「確証バイアス」と呼びます。
確証バイアスは試験の見直しのときだけでなく、実に多様に、そして当たり前に私達の日常生活に含まれています。
例えば、皆さんが友達から次のような相談をされたとしましょう。
「今 B君と付き合っているんだけど、最近お金をせがまれるようになったんだよね・・・。どこか一緒に出かけても1円も払ってくれないし。機嫌悪くなると物に当たったりするから、ちょっと怖くて・・・」
皆さんの立場から見ると、これは到底良い関係とは思えないので、「そんな人とは別れたほうが良いよ」と伝えたとします。
そのような時、往々にして次のような回答が返ってくることがあります。
「いや、でも本当はいい人なんだよ」
このように「相手はいい人だ」というのが相談者が持っている確証バイアスです。
勿論付き合いの中で、デートを共に楽しんだり、優しくしてもらったことも事実でしょう。
しかし起こった出来事の中で、そういった「相手はいい人である」という出来事のみを抽出して、それ以外の嫌な出来事をすべて「例外」として捉え、軽視してしまうのです。
なぜそういった思考になるかというと、この場合、「相手は良い人」にしないと、それまで付き合ってきた自分の行動や考えが否定されてしまうからです。

「間違っている前提」で見直しをする批判的思考を身につける
さて、ちょっと話が大きくなりましたが、では、こういった確証バイアスを試験のときに避けるにはどうすればいいでしょうか?
有効なのは、実験にもあるように「自分が間違っている前提」で見直しをすることです。クリティカル・シンキングや批判的思考とも呼ばれています。
これをすることで自分の考えの偏りに気付き、物事をいろいろな面から見つめ直すことができます。
例えば、計算問題を見直す時、なんとなく「あってる、あってる」と無意識に考えていませんか?そうではなく、「自分は絶対この問題ミスをしている」と考えて探すのです。
具体例として、次のような問題のときの批判的思考を載せておきます。
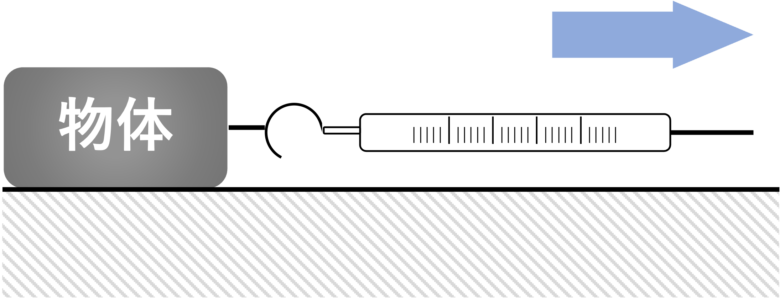
摩擦のある床に置いてある物体を毎秒4cmの一定の早さで矢印の方向に引いた。このときばねばかりは16Nを示していた。
この物体を2秒間引いた場合、物体がされた仕事は何Jか求めよ。
✕ 2秒間×4cm だから 8cm物体は進んでいる。加えた力は16Nだから、8×16で答えは128Jだ。よし計算も間違っていないな。OK
◯ 2秒間×4cm だから 8cm物体は進んでいる。だが、これが間違っているとしたら、どこだろうか?秒数を間違えているか?距離を間違えているか?はたまた単位を見落としていないか。2×4は本当に8なのか?・・・うん、どれも間違っていないな。
次に、加えた力は16Nだから、8×16で答えは128Jだ。さて、これも間違っている前提で考えると、間違える可能性があるのは、計算、単位だ。8×16 は 8×8×2 と正しくなるはず。すると、64×2で、確かに計算は間違っていない。
次は単位だ。8cm という単位が間違っているとすると、考えられるのは、m や km、あるいは mm などで J は計算するということだ。実際に J の計算は・・・・はっ!J = N × m だから、単位が違うじゃないか!となると、正しくは 0.08×16 = 1.28J だ!
さて、問題は本当に「J」を聞いているだろうか。うん、これも確実に問題文に「仕事をJで表す」ように指定されている。よし、OK。
このようにテストの最後に見直しを行うことで、ほとんどのケアレスミスを無くすことができます。
もちろん、何度も練習してトレーニングを積む必要がありますが、色々なところで使え、かつ万能です。
自分の教え子も特に知識量が増えたとかではないにもかかわらず、クリティカル・シンキングを実施することで、20点以上点数が上がったケースも珍しくありません。
まとめ:見直しのときには批判的思考をしよう!
残念ながら、この確証バイアスから逃げられる人は一人もいません。皆大なり小なり、このバイアスを持って生活しています。
しかし、自分がこのバイアスを持っていること。そして、このバイアスに陥らないように批判的思考をしようと心がけるだけで、このワナに陥らずに済みます。
皆さんも、試験の見直しの際には確証バイアスに陥らないように注意してくださいね。

今回の実験は、「Think right」という書籍で紹介されていたものだよ。他にも「平均への回帰のワナ」や「サンクコストのワナ」など面白い話が沢山載っているので、興味を持った人は是非読んでみてね!