こんにちは、ぺそです!今日は「図形の合同証明」を解く力が、どのように役に立つのかを見ていきたいと思います。
今回は中学校のときに学んだ「三角形の合同条件」を例に見ていきましょう。
また、事業分析やマーケティング分析などに使うフレームワーク「3C」も例に出しますので、その解説も載せておきます。(どちらもご存じの方は、両方の説明を飛ばし、こちらからご覧ください)

中学校で学んだ合同証明の考え方が、まさか事業戦略に役に立つなんて驚きだね!
復習:三角形の合同条件
それでは、まずは三角形の合同条件からおさらいしていきましょう。
3組の辺がそれぞれ等しい(三辺相等)
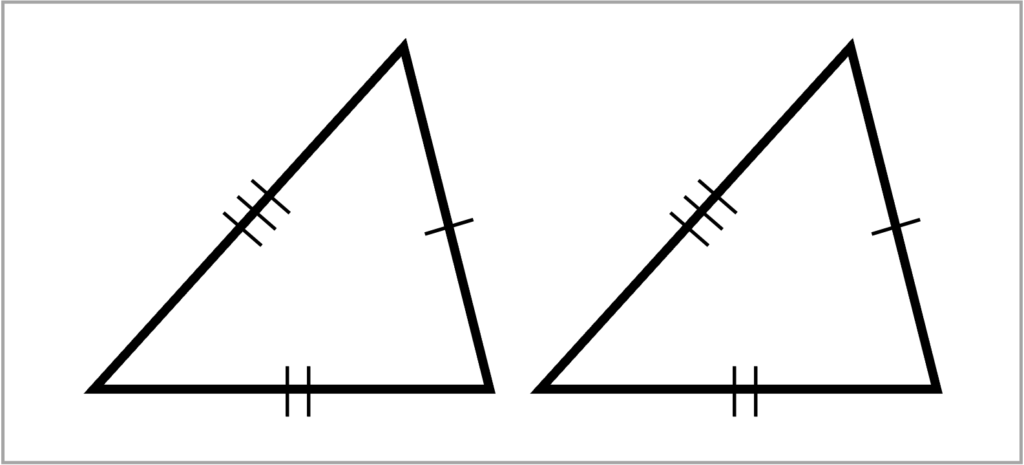
まずは、シンプルな三辺相等です。3つの辺の長さが決まると、三角形は1通りに決まるので、もし2つの三角形で3つ辺の長さがそれぞれ等しいならば、その2つの三角形は合同となります。
2組の辺とその間の角がそれぞれ等しい(二辺挟角相等)
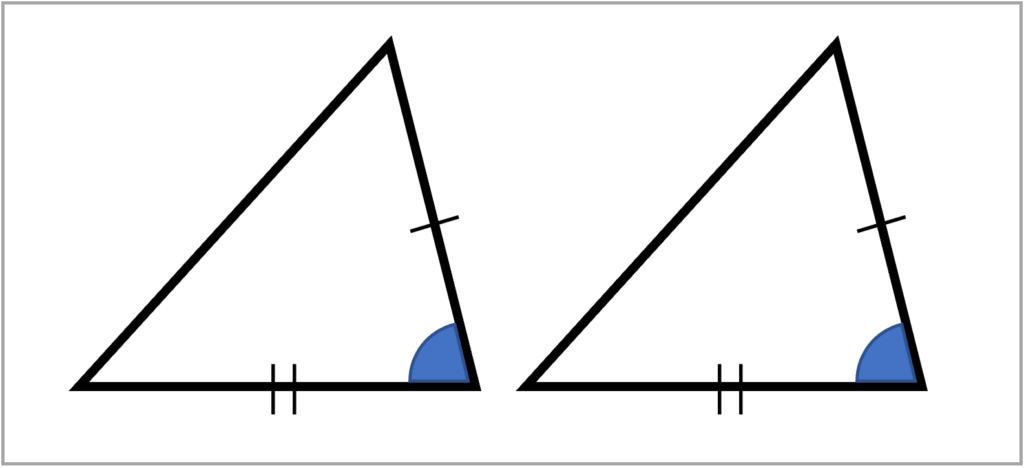
続いては、二辺挟角相等です。これも2つの辺の長さとその間の角の大きさが決まれば、三角形は1通りに決まります。したがって、この条件を満たすことでも、2つの三角形は合同だと言えます。
1組の辺とその両端の角がそれぞれ等しい(一辺両端角相等)
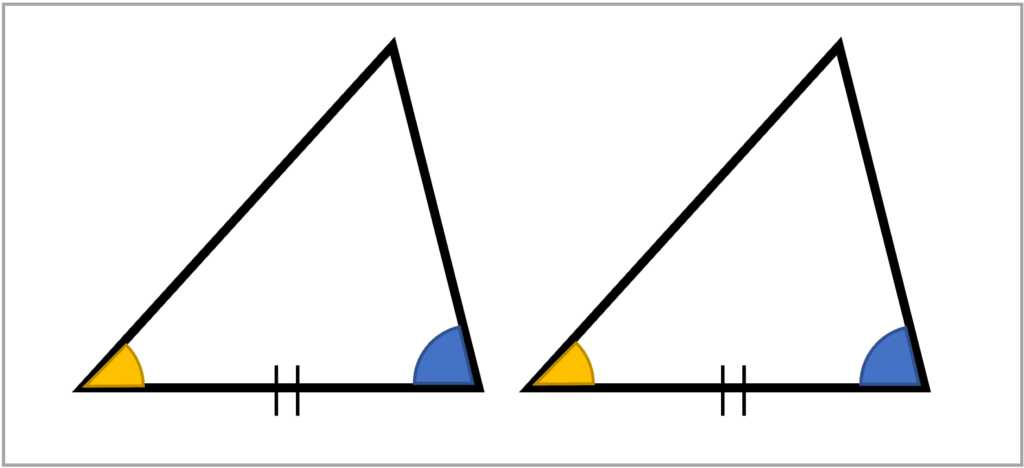
最後は、一辺両端角相等です。いままでと同様、これも1つの辺の長さとその両端の角の大きさが決まると、三角形は1通りに決まるので、この条件を満たせば、2つの三角形は合同になります。
ここまでは、大丈夫でしたか?続いて耳慣れない 3C についても見てみましょう。
説明:3C分析
続いては、3C の説明です。学生の方は聞き馴染みがないと思いますが、マーケティングや市場分析、施策検討などにおいて、非常に有名なフレームワークになっています。
3C分析とは、Customer(市場・顧客)、Company(自社)、Competitor(競合)という 3つの「C」について分析する方法です。
提唱したのは、マッキンゼーの経営コンサルタントだった大前研一氏で、その著書である『The Mind of the Strategist』(1982年)で紹介されてから、世界的に広く知られるようになりました。
どういうときに有用に使えるのかを考えるために、あなたが喫茶店のオーナーになりたいと仮定して、3C 分析をやってみましょう。
Customer(市場・顧客)
まずは、顧客について考えます。いくらやりたいことがあっても、誰も求めていないことをやっても、事業としてうまくいきません。
そこで喫茶店「市場」を見てみましょう。喫茶店業界を見てみると、2019年の「喫茶店」の市場規模は1兆1780億円もあり、十分な規模があります。
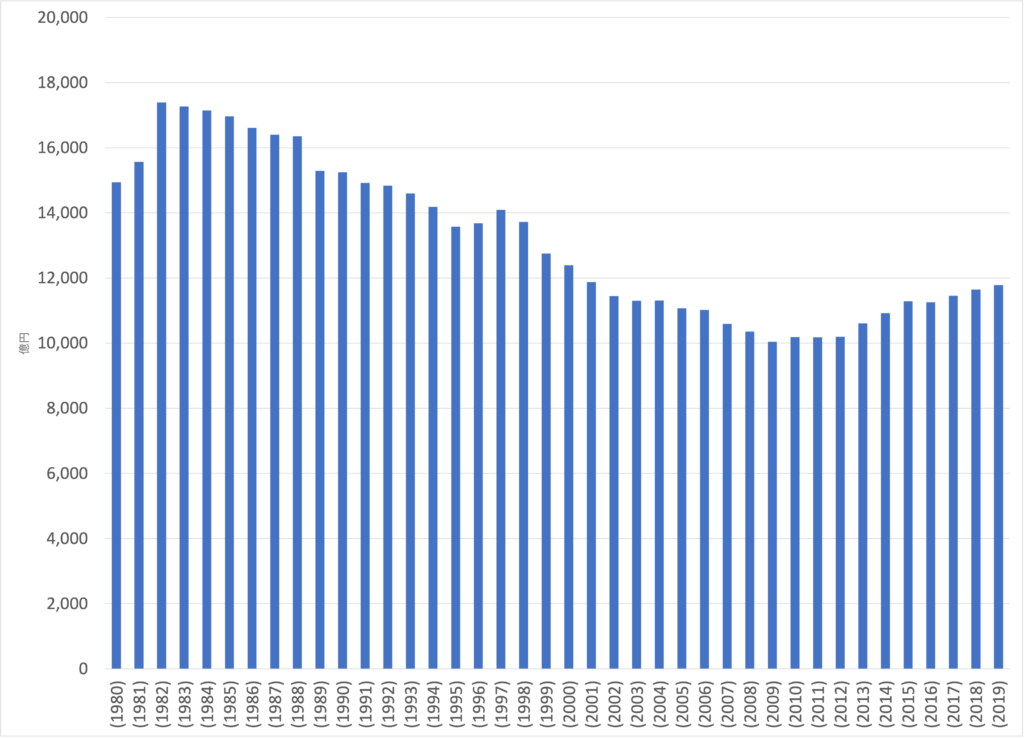
1980年から見ると下がっているようですが、10年前と比較すると約17%増加しています。ちなみに外食産業全体では、同じ10年間で約10%増です。他の外食関連よりはカフェの方が良さそうで、市場ニーズ自体はありそうですね。
つづいて顧客のニーズを考えましょう。ここでは顧客はどんなニーズを持っているかを考えます。例えば、

「安いコーヒーが飲みたい」
「美味しいオムライスが好きだ」
「長居して勉強できる所が良い」
「落ち着いた雰囲気が理想」 …etc
ちょっと思いつくだけでも、たくさんありますね。実際にはアンケートや市場調査などをして、本当にそのニーズがあるかどうか、検討していくわけですね。
以上を通して、自分たちが提供しようとしている喫茶店に価値があることを確認するわけです。
Competitor(競合)
続いては、競合を見ていきましょう。ここでは、皆さんよくご存知のスターバックスとドドールの両者について、顧客イメージアンケートから見えてきた特徴を書いてみます。
- ドトール・・・「入りやすい」「庶民的」「価格低」
- スターバックス・・・「高級感」「おしゃれ」「価格高」
※ 参考:「ブランドなんでもランキング – 好きなカフェとそのイメージ」より
同じコーヒーチェーンであっても、全然違いますね。つまり、彼らは同じ珈琲好きであっても、別々の顧客をターゲットにしているわけです。
競合調査をするのも非常に大事です。なぜなら、競合の提供価値や強みと真正面からぶつかるのは、得策ではないからです。二番煎じになりますし、オリジナリティも出ません。顧客としても、同じニーズが満たされるなら、より信頼がある方を選ぶでしょう。
そこで、自社の提供できる価値について考える Company の出番になります。
Company(自社)
最後に自社です。自分がどんなカフェにしたいのか、顧客に何が提供できるのか、そしてそれが競合と差別化できているか、などを見ていくわけですね。基本的には、
- [顧客]が求めているのに[自社]が提供できず、[競合]が提供できている:弱み
- [顧客]が求めているのに[競合]が提供できず、[自社]が提供できる:強み
となります。例えば CM をやろうと思っても、自社は現在 1店舗目をオープンしようというところで、資金力がありません。むしろ大企業のほうが TV CM の効果は大きく、やらないほうがいいでしょう。
一方、そういったチェーン店は個別の店舗戦略が難しいです。例えば 1店舗だけ内装や外観を変えたりすることは、全体のブランドを損なうため、非常にやりづらいです。逆に自社は 1店舗なので、思うがままです。これは自社の強みになります。
こうやって、3C を通して弱みを克服し、自社だけの強みを発揮していくのが事業の基本となります。したがって 3C を作りあげるのは、決してすぐにできるわけではありません。

「珈琲が安い[自社]だけだと、ドトール[競合]の強みと被ってしまう。むしろ、音楽とカフェというところに注目して、音楽好きが集まるカフェ[自社]とかどうだろう。でもそうするとターゲットがすごい少なくなるな。いま店を出展しようとしている近辺で、音楽が好き + 珈琲も飲みたい人はどれだけいるだろう?[市場]」
こんな感じで何度も何度も3つの項目を行ったり来たりしながら、最終的にはシンプルで分かりやすい3Cが出来上がるのです。
合同証明と3C分析思考の共通点
これで、三角形の合同条件と3C分析について理解できましたね。それでは、具体的に合同証明問題の解き方と3C分析のやり方の共通点について、整理して見ていきましょう。
段階①:情報をそのまま使う
これは非常に簡単です。三角形の証明なら、3つの証明条件から当てはまるものを使う。3C 分析では 3C というフレームワークを使うというだけですね。
問題で例えると、次のようなケースです。
Q. 次の 2つの三角形が合同であることを証明せよ
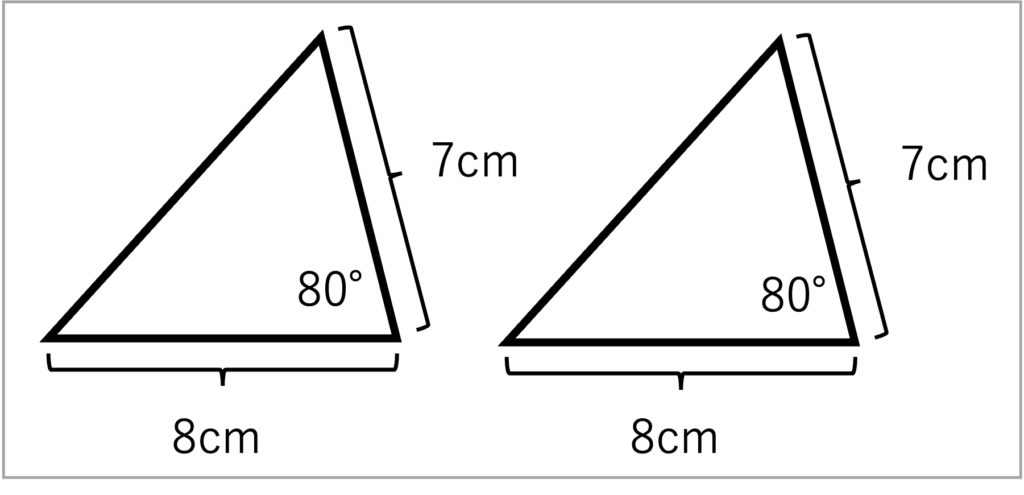
二辺挟角相等により、合同
シンプルですね(笑)
3C だと、こんな感じです。
Q. 喫茶店事業をやったほうが良いかを答えよ
Company:コーヒーを提供できるノウハウがある
Customer:皆がコーヒーを飲みたがっている
Competitor:誰もコーヒーを提供していない
3C分析により強みしかないので、やった方が良い
しかし、世の中そんなに甘くありません(泣)。受験で上記のような問題は出ないでしょうし、そんな楽な事業があれば、もう既に誰かがやっているでしょう。
そこで、多くの場合は段階②を行う必要があります。
段階②:与えられた情報を使えるように、新たに考える
今度は、よく目にするような次の証明問題を解いてみましょう。
Q. △ABCと△DCBが合同であることを証明せよ
(仮定:∠ABC = ∠DCB, ∠BAC = ∠CDB)
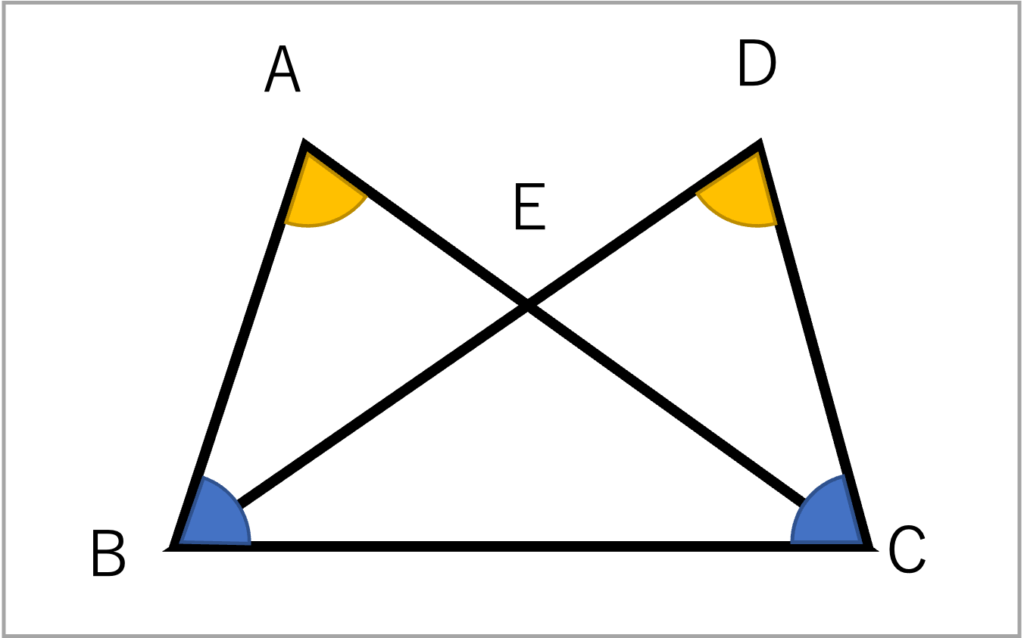
BC はどちらも同じ辺。またその片方の角度も ∠ABC と ∠DCB は等しいと与えられている。この情報だけでは、証明をすぐに解くことはできない。
あとは、合同を証明するには、∠ACB=∠DBCと言えれば一辺両端角相等で合同と言えるし、AB=DCと言えれば、二辺挟角相等で合同と言える。
AB=DC に関しては、辺の長さがまったく与えられていないので厳しそうだ。一方角度は既に2つのところで等しいのがわかっている。
三角形において、内角の和は常に一定(180°)だ。つまり、もし2つの角が等しいなら、残りの1つの角も等しくなる。つまり、
∠ACB = 180°-(∠BAC🟠 + ∠ABC🔵)
= 180°-(∠CDB🟠 + ∠DCB🔵)
= ∠DBC
したがって、∠ABC = ∠DCB, BC = CB, ∠ACB = ∠DBC より一辺両端角相等で合同
この問題は、与えられた情報だけでは、解けませんでしたね。三角形の内角の和は常に同じあることから「三角形において、2つの角が等しいなら、残りの1つの角も等しい」という、新たな視点から導くことが必要でした。
3C 分析も同様です。
Q. 喫茶店事業をやったほうが良いかを答えよ
Company:コーヒーを提供できるノウハウがある
Customer:皆がコーヒーを飲みたがっている
Competitor:コーヒーを既に提供している
現状の3Cでは喫茶店はやらないほうがいいとなる。しかし、Customer をより深く分解しきれていない可能性が高いので、そこを深堀ることにする。
あとは、事業をやったほうがいいと言えるには、他社にはない強みがあると言えれば良い。
コーヒーに関しては、どこも提供しているので、自分のノウハウでは競合を超えるのは厳しそうだ。一方、顧客が本当にコーヒーを飲みたいだけならば、自宅のインスタントでも良いはずで、他にもニーズがあるはずだ。
顧客ニーズは一つとは限らず、常に多様だ。つまり、コーヒー以外のニーズで他の競合が満たせず、自社だけが満たせるニーズがあるならば、十分事業してやる意味はあるはず。
例えば、一般的なコーヒー店では、BGM は基本的に雰囲気を作り上げるもので、顧客の会話を邪魔しないように流されている。一方、自分は音楽に詳しく、趣味で沢山のレコードも持っている。音響にも詳しいし、他社では提供できない音楽の楽しみを提供できるだろう。
そこで改めて上記の視点で、3Cを整理してみる。
Company:コーヒーだけでなく、本格的な音楽を提供することができる
Customer:コーヒーを飲みながら、音楽に没頭したい
Competitor:コーヒーは提供しているが、音楽はおまけに過ぎない
したがって、顧客の中で「音楽に本当に耳を凝らしながらのコーヒーを楽しみたい」というニーズがあり、自分がその音楽を提供することができるなら、事業としてやってみてもよい。
はい、これも新たな視点が必要でした。
先ほどと同様に、与えらた情報ではどうしようもありませんでした。しかし「もし、顧客が別のことを欲しがっていたら」と、新たな視点を導入することで、事業として成り立つ可能性が出てきました。
実際に、これはミュージックカフェとして一つの地位を築いていますね。

【まとめ】情報を整理し、視点を増やし、結論を出す
というわけで、今回は三角形の合同条件と3Cについて見てみましたが、思考の仕方が意外と共通していたのが分かるでしょうか?
「まずは情報を集める」ところからはじまり、情報量が不足していれば、「持っている知識を用いて情報を増やせないか、新たな視点はないかを考え」、最終的には「適切な結論を出す」。
この考え方は基本的に全てにおいて同様です。他にもマーケティングをやるときには、SWOT 分析、PEST 分析、5フォース分析など、沢山のフレームワークがあります。
それらを違和感なく使える人は、そのような基本の思考方法が身についている人です。
一方、都度都度立ち止まってしまう人は、そのフレームワークでしか役に立たない考え方をしている人です。三角形の合同証明を覚えていても対して役に立ちませんが、情報の増やし方や視点の変え方を覚えている人は、色々なときに役に立ちます。
是非皆さんも、図形の証明問題を解くときには、「あー、こうやって新たな情報を得ることができるんだな」という点に着目して、解いてみてください!