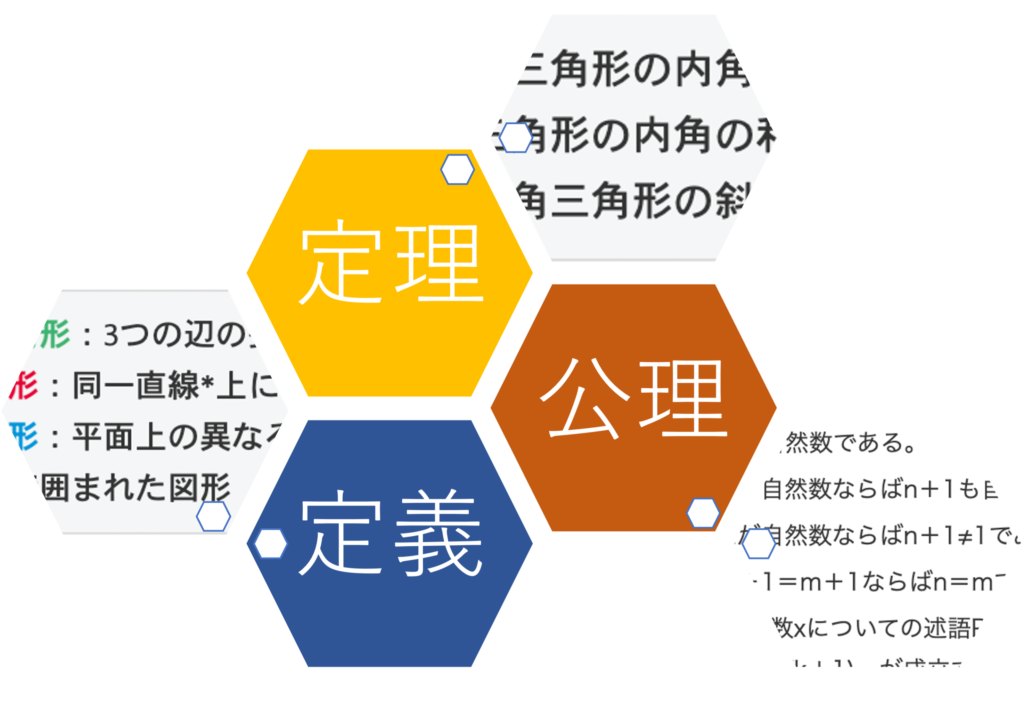
こんにちは、ぺそです!今回は、意外と混同しがちな「定義」「定理」「公理」の違いについて解説しようと思います。実はこの3つ似ているようで、異なる意味を持つため、しっかり使い分けできることが大切です。
片方は定義のつもりで喋っていたのに、実はそれが定理だったら・・・そんな行き違いを起こさないように、本記事でそれぞれの違いをしっかり確認しておきましょう。
「定義」:ある概念の内容やある言葉の意味を他の概念や言葉と区別できるように明確に限定されたもの
定義とは、「ある概念の内容やある言葉の意味を他の概念や言葉と区別できるように明確に限定されたもの」を指します。
ちょっと難しいので、具体例をみてみましょう。例えば、次のようなものが定義になります。
正三角形:3つの辺の長さが等しい三角形 学生:主に学校やその他の教育機関に入学して、知識を習得し、職能を開発し、特定分野での雇用を得やすくすることを目的に学習している者
これらは、定義になります。わかりやすくいうと、定義は人間が色々便利なように「そう決めた」というものです。
従って、定義は「証明できません」。あくまで決めの問題だからです。
また、定義があることで、その定義を使って新しい定義が誕生することもあります。例えば、先程の正三角形では、下記のように定義の数珠つなぎになっています。
正三角形:3つの辺の長さが等しい三角形
三角形:同一直線*上にない3点と、それらを結ぶ3つの線分からなる多角形
多角形:平面上の異なる 3個以上の点と,それらを結ぶ線分からなる,閉じた単純折れ線で囲まれた図形
※ ここで出てくる「直線」は、実は「公理」になります。詳しくは後ほどできてくる公理をご覧ください。
また大事な点として、基本的に定義は「一つに付き一つ」です。これは、複数の定義があると、使い方などによって矛盾が生じてしまうからです。
同音異義語等の場合は複数あるように見えますが、これらは本質的に別のものを指しているため、その場合は問題ありません。

例えば、川を渡る「はし」と、食事を作るときに使う「はし」は、別の定義がされているけど、漢字で書くと、もともと異なる単語(橋と箸)で、発音がたまたま一緒だということが分かるよね。この場合は、たまたま音が一致しただけなので、定義として矛盾しないんだ
「定理」:定義や公理から証明することができるもの
続いては定理です。定理は「定義や公理から証明することができるもの」です。
こちらも例を見てみましょう。定理の例としては、以下のようなものがあります。
・正三角形の内角はどれも等しい ・三角形の内角の和は180度になる ・直角三角形の斜辺の2乗が他の辺の2乗の和に等しい(三平方の定理)
ポイントは、定理は、定義と既に証明された別の定理を用いて証明することができるという点です。
例えば、「正三角形の内角はどれも等しい」について使って証明してみます。あえて数学的記号はできるだけ使わずに、文章で説明すると、
1. 正三角形は2つの辺が等しい二等辺三角形である。 2. 二等辺三角形の底角は等しい。 3. それぞれの底辺からみた 3パターンを考えてみると、全ての底角が等しくなる → よって、正三角形の内角はどれも等しくなる
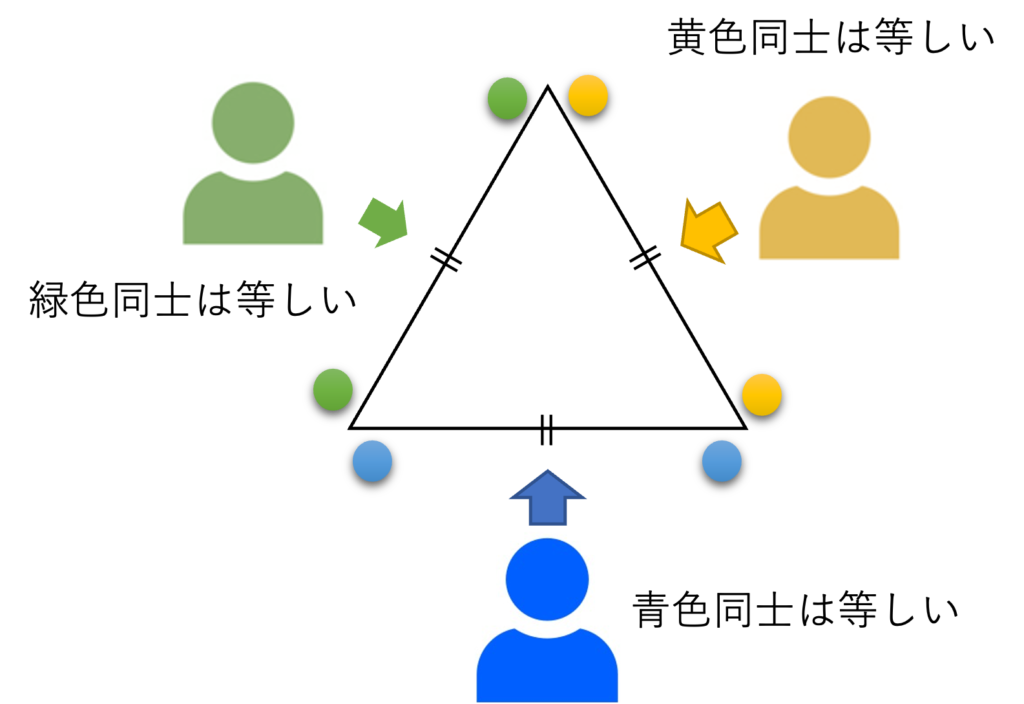
今回の証明で出てきた定義と定理を分類すると、こうなります。
- 正三角形
- 二等辺三角形
- 底角
- 内角
- 底辺
- 二等辺三角形の底角は等しい
それぞれの言葉が定義されていて、既に二等辺三角形の底角が等しいという定理が証明されているので、それを使って別の定理の証明ができたわけですね。
「公理」:ある理論の出発点となる仮定
最後は公理です。多くの人は、定義と定理については知っていても、「公理」に関してはあまり知らない方も多いんじゃないでしょうか。
ですが、実は「公理」が数学に置いては最も重要であったりします。
「公理」とは、「これは証明できないけれど、正しいと仮定して論理の出発点におくもの」になります。
「定理」と比べると、公理は証明できない <=> 定理は証明できるという違いがあります。一見便利な公理ですが、何でもかんでも公理としてしまうと、実は正しくなかった場合には、その上に成り立つ全ての定理や定義が崩れ去ってしまいます。
また、現状必要な公理は既に出揃っているので、一般的には私達が公理を考え出すことは、ほとんどありません(というより、公理自体を考えることがないですよね(笑))。
定理の例としては、例えば自然数論において有名なペアノの公理があります。
- 1は自然数である。
- nが自然数ならばn+1も自然数である。
- nが自然数ならばn+1≠1である。
- n+1=m+1ならばn=mである。
- 自然数xについての述語P(x)について、P(1)および「任意の自然数kについてP(k)ならばP(k+1)」が成立すれば、すべての自然数nについてP(n)である。
一番下はちょっと難しいですが、それ以外は見て「そりゃそうだ」となりますよね。ですが、「証明しろ!」と言われると難儀するものばかりです。…というかできません(笑)。
けれども、この 5つの公理があって、初めて「自然数」が定義できるのです。この5つの公理を満たすものが自然数であるという定義ですね。
また、公理は証明できないので、皆さんはいちいち証明しなくていいわけです。
おまけ:『なぜ「1+1=2」なの?』
よく「なぜ 1+1=2 になるのですか?」という質問がありますが、実は「そういうふうに仮定した数字を2と置いたから(公理的説明)」であったり、「そういう風に2という数字を定義したから(定義的説明)」というのが、回答として正しいのです。
定理であれば証明できるので、「なぜ?」に答えられることが大事です。
しかし、定義や公理として決めたことに関しては、「そうするのが人間の都合がいいから」というのが、逃げでもなんでもなく、きちんとした答えになります。

もちろん「何でそう決めた方が都合がいいんだろう」には答えられると、もっといいけどね。
【まとめ】定義・定理・公理の関係性
少し話が逸れましたが、まとめると基本的な三者の関係は、下記のようになります。
「公理(証明できないが、正しいだろうと言える仮説)」
→「定義(定理が正しい前提で、使いやすいように決めた言葉)」
→「定理(定義や公理から導き出された、証明できる論理)」
さて、今回で3つの意味を理解したとこで、実生活にどう役に立つのでしょうか?
実は人と話して話が合わないときに、この 3つのどれだと思って話しているのかがずれているケースが良くあります。
それを知ると「なぜ意見が異なっているのか」、そして「どう合意形成をするのか」において役に立つので、機会があったら、その点についても触れていきたいと思います。