私たちは日常生活の色々な所で確率を用いて、自分が取る行動を選択しています。
わかりやすい例だと、天気予報や、ソーシャルゲームのガチャがありますね。他にも、ガン保険なども「将来自分がガンになる確率」を天秤にかけて毎月の保険料を支払うわけです。
だからこそ、私たちは確率をきちんと理解しないといけませんし、多くの人は数学の授業で確率について学んでいます。にも関わらず、確率の数字を正しく捉えられている人は非常に少ないのです。
では、私たちは確率の一体何を誤解しているのでしょうか?また、何に気をつければ正しく理解できるようになるのでしょうか?

確率を間違って理解していると、知らず知らずのうちに誤った選択をしちゃうことになるから、是非この記事を参考にして、数字上の見た目に騙されないようになろう!
説明を変えただけで、患者の捉え方が変わった
ここでとある精神分析医の話を紹介しましょう。
この医者は軽度のうつ病患者に抗うつ剤を処方していました。薬には副作用が起こる可能性があったため、当然医者は患者にその副作用について丁寧に説明をしていました。
その中の副作用に性欲減退・性交不能が含まれていたので、医者は次のように説明しました。

この薬を飲むと、セックスに関する問題が起きる可能性が30%から50%あります。
これを聞いた患者の多くは、不安になり、薬を飲みたくないと嫌がりました。ここで、この医者はある問題点に気づき、言い方を次のように変えたのです。

この薬を10人の患者さんに処方すると、3人から5人がセックスに関する問題を報告してきます。
すると一部の患者で薬の服用に対する不安がやわらいだのです。
どちらの発言も見比べてみると確率的には全く同じことを言っているように見えます。しかし、これを聞いた患者の行動は異なっているのです。
これは一体なぜなのでしょうか?

その確率は単一事象?それとも頻度?
この違いは、聞いた確率を「単一事象」として捉えているか、「頻度」として捉えているかです。
元々の説明では、患者は「自分が性行為をするときに30~50%失敗する」と思っていました。これが単一事象の捉え方です。
単一事象では、確率を一つの事象で起こることと捉え、その割合を確率として見ます。この考え方をする場合、どんなに低い確率でも、その数字が自分を基準としているため、どれだけ楽観的な人でも不安に駆られるでしょう。
一方後者の聞き方は「頻度」を表しています。「〇〇人のうち〜」という言い方をすることで、大勢の対象の中にいる自分が想像できます。
このように基準となる集合が明示されることになるので、より正確に事象を理解し、正しく判断することができるのです。

数学リテラシーの高さは関係ない
「自分は数学苦手だから、ちょっと難しいかも…」と思った人もいるかもしれません。しかし、この確率に対する理解力と数学リテラシーの高さには、そこまで相関がないことがわかっています。
先ほどの例にあった聞き方を数学リテラシーがある人/ない人に分けて質問した結果を分けたのが次の表です。
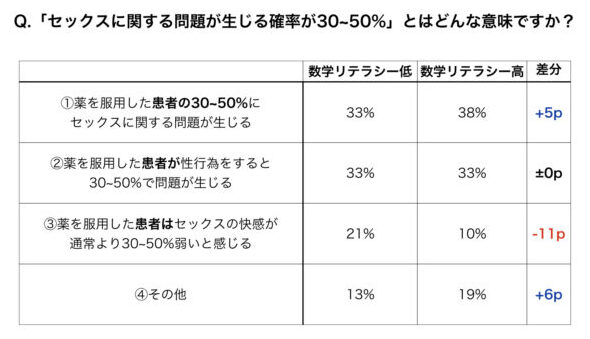
みなさんもここまでの話を見れば、①が正しいことがわかると思います。②は単一事象で捉えており、③に至っては全く別のことを言っています。
ここで数学リテラシーとの差異を見比べてみると、数学リテラシーが高くても正しく理解している人は38%に過ぎず、低い人と大差ないことがわかります。
つまり、確率を正しく理解するのに大事なのは、数学リテラシーではないということです。

数学が苦手かどうかではなくて、「単一事象と頻度の違い」を知っているかどうかの方が、確率を理解するには大事なんだね!
なぜ、確率に注意する必要があるのか
同様のことはいろいろな所で起こっています。ここでは二つの例を見て見ましょう。
例題①:起業の2割は失敗する
例えば、みなさんが学生のうちから起業しようと考えたとします。そんな時に、過去のデータを使って「5年以内の起業の失敗率は18.3%。2割近く失敗するんだからやめた方が良い(出典:2017年版中小企業白書)」と言われました。
しかし、これはあなたが失敗する確率(単一事象)ではありません。そうではなく、100人の起業家を集めたうちの18人が失敗したという確率(頻度) です。
この100名には当然色々な人が含まれています。
もちろん才能があったのに失敗した人もいるでしょうが、中には甘い考えで起業しただけの人や、とりあえず起業したみたというだけの人もいるはずです。
ですから、もしあなたが起業をしたいなら、こういった数字に踊らされる必要はありません。是非起業にチャレンジして見てください。
例題②:二人は一人はガンになる
確率は非常にわかりやすく、インパクトもあるため、各種商品やサービスのプロモーションでもよく使われます。
冒頭でガン保険について触れましたが、みなさんも「二人に一人はガンになる」というフレーズを耳にしたことがあるかもしれません。
一見正しく頻度で確率を表しているように見えますが、果たして本当にそうでしょうか?
実はこれ、正しくは「生涯でガンと診断される確率」なんです。実際のデータで確認しましょう。
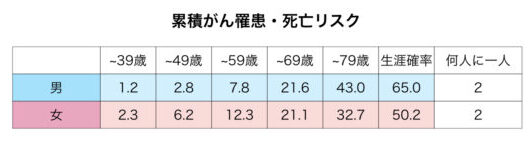
引用:国立がん研究センターがん対策情報センター
このように、実際には年齢とともにガンと診断されるケースが増えていることがわかります。これを「今の自分がガンにかかる確率」だと思ってしまうと、まんまとプロモーションに踊らされていることになります。
さらに母集団をよく見ると、対象が「羅患・死亡」となっていますから、「ガンと診断される = 死亡」とは限らないことも分かります。
試しに死亡率だけで見てみると、~69歳までは、男性が5.5%/女性が3.9%となっており、イメージとだいぶ違うことがわかります。
従って、確率を使って判断をするときは、このように母集団を正確に理解することが必要です。その上で必要なサービスを選ぶのが賢明でしょう。
[まとめ] 確率を見た時は、単一事象なのか頻度なのかを必ずチェックし、その母集団を理解しよう
いかがでしょうか?確率の計算ができることも大事ですか、それ以上に確率をどう使うかの方が大事です。
今後確率に出会ったときは、それが単一事象なのか、頻度なのか。そして母集団はどうなっているのかについて意識を向けて見ましょう。それだけで、確率を正しく捉えることができるようになります。
さて、明日の天気予報の雨の確率はどちらでしょう?

今回紹介した話は「賢く決めるリスク思考」という書籍に載っているので、もっと詳しく知りたい!と思った人は、是非読んでみてね